Standards of Mathematical Practices - Part 3
- Chris Greene
- Jan 19, 2018
- 4 min read
Mathematical Practice #2 - Reason Abstractly and Quantitatively
One difficult area for students to grasp is the ability to make connections between quantities of a situation and the understanding how these quantities relate to being able to solve a problem. Understanding the importance of labeling the quantities in the problem, labeling during the problem solving process, and labeling the quantity of the solution help students during the entire problem solving process. The students who are not proficient in this skill seem to lack the comprehension of the problem and then connecting the meaning of the solution to the context of the problem. Building reasoning through concrete problems can help students to begin to reason abstractly, which in turn makes them better problem solvers. For example, students need to understand that labeling measurement units in a problem provides meaning to the numbers that are being utilized to solve a problem. Making connections from the abstract numbers to quantities develops over time. This starts at an early age. Observing how young students solve the following type of problem gives an interesting peak into their thinking.
Four friends go to the grocery store to buy fruit. Fred chooses to buy 4 apples. Derek buys 5 apples. Trey loves apples so he buys 8 apples. Lastly, Rick decides to buy 3 oranges. The four friends buy a total number of ____ apples.
As the student solves the problem and just adds all the numbers in the problem, this lack of connection between the meaning of the quantities and the question being posed is troublesome. Providing these types of distractors in problems force students to make a connection between the quantities in the problem and what is needed to solve the problem. Whether a student is working a problem individually or in a group, each student needs to be held accountable for understanding the entire process and the meaning of all the quantities in relation to the situation. As students discuss and present solution paths, we need to have students ask clarifying questions to students as they are explaining. Teachers can help prepare students for this type of questioning by giving sentence starts for students to ask questions (Accountable Talk). Listening to their responses will provide vital feedback for the teacher to have a grasp of the student's understanding of the problem.
As students develop the understanding of what to ask other students about their work, this will bleed over into developing their own problem solving techniques. I have noticed that students starting to ask themselves the same types of questions as they are solving problems to clarify their own work to see if the work make sense. As the year progresses and we practice more with these concepts, these types of behaviors become the norm within the classroom.
Connections between the meaning of quantities and the problem at hand leads into developing abstract reasoning to solve problems. One of my favor topics to teach is quadratic functions. Problems like the following gave me insight into how students try to answer a problem abstractly without connecting the meaning of the information in the problem to the topic of study.
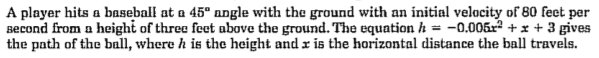
Question: What is the maximum height reached by the baseball?
As I have observed the majority of students try to solve the problem, the students start to use either the quadratic formula or a method they had been taught to find the axis of symmetry. When they do not understand the meaning of the values they are finding, then the values they are finding just become a guess when I ask them their answer. There are a limited number of students trying to put meaning to the quantities in the problem. These students are sketching a representation of the situation and discussing a plan of attack to solve the problem. After this prep work for the problem, the question was answered very easily. Many groups struggled with the problem due to the fact that they were not putting meaning to the elements of the problem. When students presented their work to the class and their classmates asked questions about their process and drawings, a clear picture began to develop for all the students. This is a topic that is taught in the 2nd semester in my class and we have utilized many strategies to help with problem solving throughout the year, but until word problems are presented to the class the application of the math topic was still abstract in nature. Posing problems or situations that force students to reasoning abstractly and quantitatively begins to develop their logical thought process.
Modeling problem solving techniques for students at an early age can put them on the right path, but adding student discussions into the structure of class helps immensely.
Food For Thought:
As you meet in your PLC and discuss student work, think about the following question:
How are we helping students to become better problem solvers when they are struggling to solve problems? [PLC Essential Question #3]










Comments